Descubriendo lo Invisible: Entropía y Dimensión Fractal en Verduras y Legumbres
En el vertiginoso mundo de la ciencia de datos, cada píxel puede convertirse en un universo de información y cada patrón aparente en un espejo de complejidad oculta. En este artículo de divulgación exploramos cómo dos métricas —la entropía, que mide la “sorpresa” de los tonos en una imagen, y la dimensión fractal, que cuantifica su intrincada autosimilitud— abren una ventana al análisis topológico de datos (TDA) y nos permiten discernir diferencias sutiles entre objetos cotidianos. A través de dos ejercicios prácticos —primero, comparando tres verduras de hoja (perejil, cilantro y apio) y luego, seis variedades de legumbres— demostraremos cómo, con unas pocas líneas de Python y herramientas como Pillow y NumPy, podemos transformar texturas en valores numéricos significativos, revelando patrones que el ojo humano solo intuye. Prepárate para descubrir cómo la combinación de matemática y computación convierte lo ordinario en extraordinario.
Introducción
El análisis topológico de datos (TDA) surge como una disciplina que combina nociones de geometría, teoría de la información y topología para comprender formas y estructuras en datos complejos. Dos de sus herramientas más accesibles y reveladoras son la entropía y la dimensión fractal, métricas que permiten traducir texturas e irregularidades en valores numéricos que facilitan la comparación y clasificación.
La entropía, originada en la teoría de la información de Claude Shannon, mide la incertidumbre o “sorpresa” asociada a la distribución de valores en un sistema. En el caso de una imagen en escala de grises, definimos un histograma normalizado ${p_i}_{i=0}^{255}$, donde
\begin{equation}
p_i = \frac{\text{número de píxeles con intensidad } i}{\text{total de píxeles}}.
\end{equation}
La entropía (H) se calcula como
\begin{equation}
H = - \sum_{i=0}^{255} p_i \,\log_2 p_i.
\end{equation}
Valores de (H) elevados indican distribuciones más uniformes y variadas (mayor complejidad en tonos), mientras que (H) bajos apuntan a imágenes homogéneas.
La dimensión fractal, por su parte, cuantifica la complejidad espacial y la autosimilitud de un objeto cuando lo observamos a distintas escalas. Bajo el método de box-counting, dividimos la imagen en cajas cuadradas de lado (\varepsilon) y contamos cuántas de ellas, (N(\varepsilon)), contienen al menos un píxel “activo” (por ejemplo, binarizado). La dimensión fractal (D) se define como el límite
\begin{equation}
D = \lim_{\varepsilon \to 0} \frac{\log N(\varepsilon)}{\log (1/\varepsilon)}.
\end{equation}
En la práctica, calculamos valores de (N(\varepsilon)) para varios (\varepsilon), trazamos (\log N) versus (\log (1/\varepsilon)) y estimamos la pendiente de la regresión lineal, que aproxima (D). Cuanto mayor es (D), más intrincada y autosimilar es la estructura.
A continuación presentamos dos ejercicios que ilustran el poder de estas métricas para distinguir objetos visualmente parecidos. En el primero exploramos tres verduras de hoja —perejil, cilantro y apio— y en el segundo analizamos seis variedades de legumbres. Cada caso mostrará cómo, pese a apariencias familiares, la entropía y la dimensión fractal revelan diferencias fundamentales en textura y complejidad, demostrando la utilidad del TDA en tareas de clasificación y descubrimiento de patrones.
Ejercicio 1: Vegetales de Hoja
Aunque el perejil, el cilantro y el apio comparten la categoría de “verduras de hoja”, sus superficies esconden diferencias sutiles que pueden pasar desapercibidas.
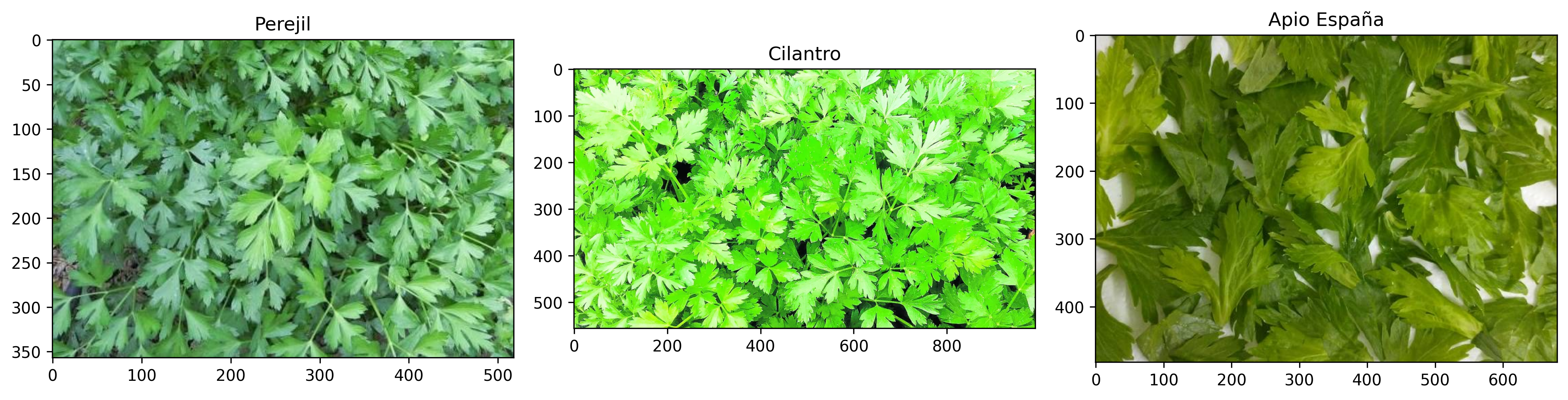
- Entropía:
- Perejil mostró el valor más alto de (H), reflejo de sus ramificaciones finas y densas.
- Apio registró el menor valor, debido a su uniformidad y planos lisos.
- Cilantro quedó en un punto intermedio, capturando su balance entre áreas densas y espacios vacíos.
- Resultados:
- La entropia del Perejil es: 7.399
- La entropia del Cilantro es: 7.388
- La entropia del Apio es: 6.952
- Dimensión Fractal (box-counting):
- El cilantro volvió a destacar, pues su entramado de hojas plegadas exhibe mayor autosimilitud a múltiples escalas que el apio y el intrincado entramado del perejil.
- Resultados:
- La Dimensión Fractal del Perejil es: 1.824
- La Dimensión Fractal del Cilantro es: 1.868
- La Dimensión Fractal del Apio es: 1.8
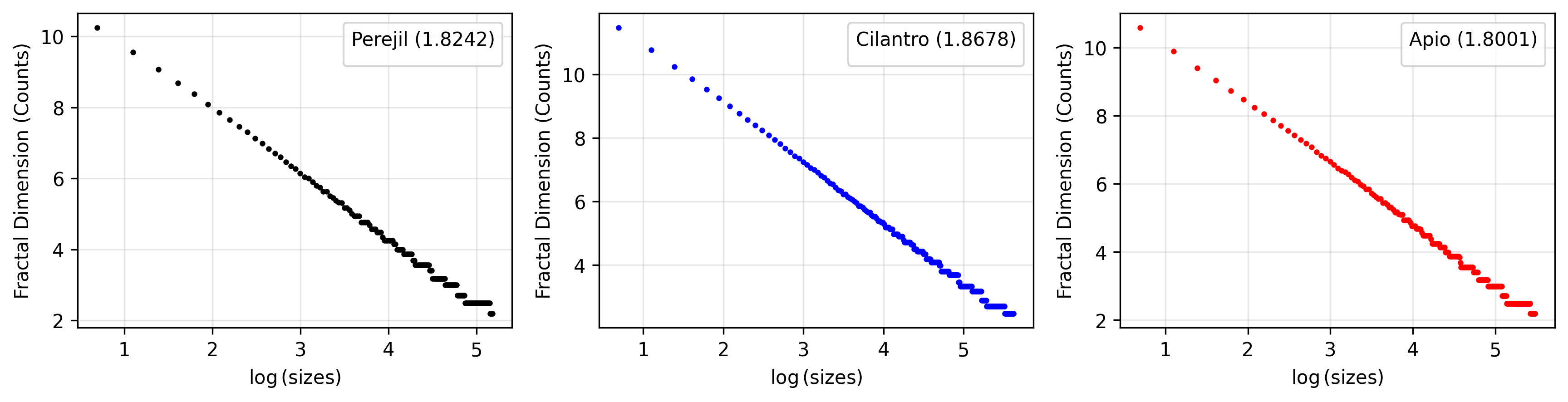
Este ejercicio demuestra cómo TDA puede revelar diferencias en objetos que, a simple vista, parecen muy similares.
Ejercicio 2: Legumbres
En el segundo ejercicio extendimos el análisis a seis variedades de legumbres: caraotas negras, rojas y blancas, lentejas, arbejas y garbanzos.

- Entropía:
- Lentejas y arbejas presentaron valores elevados de (H), por su textura rugosa y granulada.
- Garbanzos mostraron los valores más bajos, reflejando superficies más suaves.
- Caraotas negras y rojas quedaron en un rango intermedio.
- Resultados:
- La entropia de Caraotas Negras es: 7.365
- La entropia de Caraotas Rojas es: 7.716
- La entropia de Caraotas Blancas es: 6.995
- La entropia de Lentejas es: 7.446
- La entropia de Arbejas es: 7.546
- La entropia de Garbanzos es: 7.83
- Dimensión Fractal (box-counting):
- Las lentejas y las arbejas registraron las dimensiones fractales más altas, evidenciando su complejidad espacial y autosimilitud granular.
- Resultados:
- La Dimensión Fractal del Caraotas Negras es: 1.783
- La Dimensión Fractal del Caraotas Rojas es: 1.826
- La Dimensión Fractal del Caraotas Blancas es: 1.788
- La Dimensión Fractal del Lentejas es: 1.823
- La Dimensión Fractal del Arbejas es: 1.849
- La Dimensión Fractal del Garbanzos es: 1.81
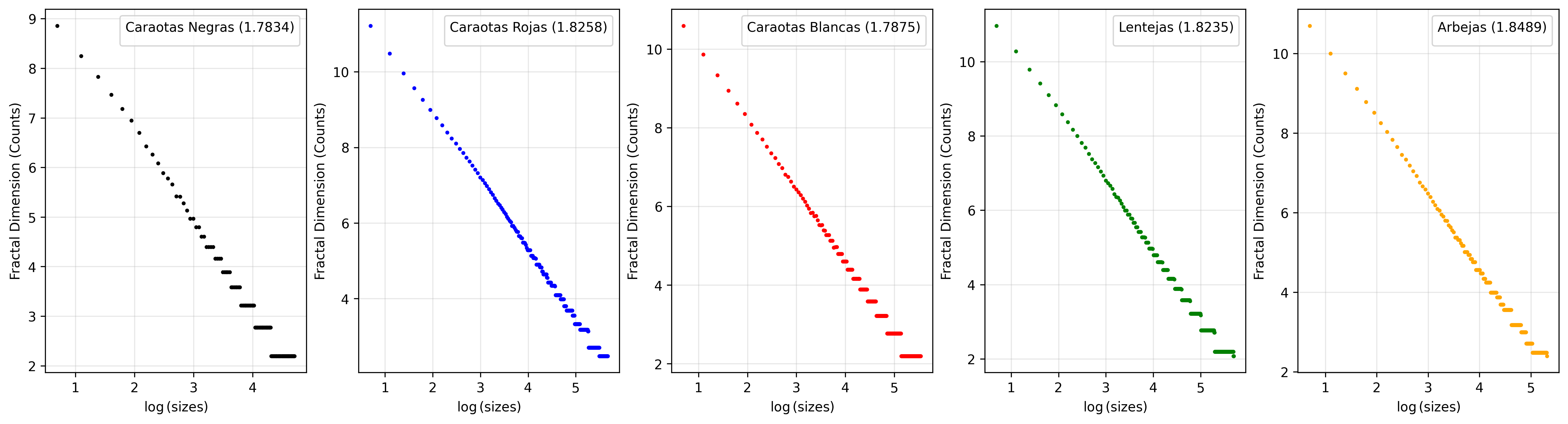
Este segundo caso reafirma que, bajo distintos lentes cuantitativos, podemos clasificar materiales naturales conforme a su textura y patrón espacial.
Esta pequeña aplicación muestra que, con unas líneas de Python y bibliotecas como Pillow y NumPy, es posible transformar texturas en datos numéricos significativos. Para estudiantes y profesores, el reto está servido: ¿qué otros patrones cotidianos podremos descifrar con entropía y dimensión fractal? El análisis topológico de datos abre un mundo donde lo aparentemente ordinario se convierte en una fuente inagotable de descubrimientos. Un pequeño Notebook de Python con estos cálculos y código para los resultados se puede encontrar en: Clasifying_images_entropy_fractal.ipynb.
Algunas referencias:
- Entropía de Shannon: Shannon, C. E. (1948). A mathematical theory of communication. The Bell system technical journal, 27(3), 379-423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x. https://ieeexplore.ieee.org/abstract/document/6773024.
- Textural Features y Entropía en Procesado de Imágenes: Haralick, R. M., Shanmugam, K., & Dinstein, I. H. (2007). Textural features for image classification. IEEE Transactions on systems, man, and cybernetics, (6), 610-621. https://doi.org/10.1109/TSMC.1973.4309314. https://ieeexplore.ieee.org/abstract/document/4309314.
- Procesado Digital de Imágenes: Gonzalez, R. C., & Woods, R. E. (2018). Digital Image Processing (4th ed.). Pearson. https://www.cl72.org/090imagePLib/books/Gonzales,Woods-Digital.Image.Processing.4th.Edition.pdf
- Dimensión Fractal y Box-Counting: Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. W. H. Freeman and Company. https://www.osti.gov/servlets/purl/138337#page=46.
- Aplicación del Método de Box-Counting: Russ, J. C. (1994). Fractal Surfaces. Springer. https://doi.org/10.1007/978-1-4899-2578-7. https://link.springer.com/book/10.1007/978-1-4899-2578-7.
- Análisis Topológico de Datos (TDA): Carlsson, G. (2009). Topology and data. Bulletin of the American Mathematical Society, 46(2), 255–308. https://www.stat.uchicago.edu/~lekheng/meetings/mmds/slides2008/carlsson.pdf
- Persistencia en TDA: Edelsbrunner, H., Letscher, D., & Zomorodian, A. (2002). Topological persistence and simplification. Discrete & Computational Geometry, 28(4), 511–533. https://doi.org/10.1007/s00454-002-2885-2. https://link.springer.com/article/10.1007/s00454-002-2885.
- Revisión de Aplicaciones de TDA en Ciencia de Datos: Ghrist, R. (2008). Barcodes: The persistent topology of data. Bulletin of the American Mathematical Society, 45(1), 61–75. https://www.ams.org/journals/bull/2008-45-01/S0273-0979-07-01191-3/.