El Mundo de Game of Thrones: Más Allá de lo Plano
Desde que era un niño, siempre me he sentido fascinado por los mundos mágicos y ficticios que habitan las historias épicas. Cada universo, con sus propias reglas, criaturas y tierras lejanas, ha sido una fuente inagotable de asombro y curiosidad. El Señor de los Anillos de J.R.R. Tolkien, con su inmenso mundo de la Tierra Media, fue uno de los primeros universos que me atrapó. La complejidad de sus mapas, las culturas, y las luchas entre el bien y el mal me inspiraron profundamente. Pero con el paso del tiempo, también me sumergí en otros mundos mágicos como La Rueda del Tiempo de Robert Jordan o Cuentos de Terramar de Ursula Le Guin, y, más recientemente, en el fascinante y crudo universo de Juego de Tronos creado por George R. R. Martin.
A lo largo de mi vida, también he sido un apasionado de las matemáticas y la ciencia. Las fórmulas, los números y los patrones que rigen el mundo real siempre han sido mi otra gran pasión. La ciencia nos permite entender cómo funciona nuestro propio universo, mientras que la fantasía nos da la oportunidad de soñar con mundos que desafían las leyes de la física y la lógica. Sin embargo, a veces me encuentro pensando que hay algo más en común entre estos mundos de ficción y la ciencia de la realidad. ¿Y si te dijera que el mundo de Juego de Tronos no es tan plano como parece? ¿Y si te demostrara que, de hecho, es una esfera?
Hoy, quiero mostrarte cómo, a través de simples conceptos matemáticos, podemos descubrir que el mundo de Juego de Tronos, ese vasto y fascinante escenario de intrigas y batallas épicas, no es simplemente plano, sino que se ajusta a la forma de una esfera. Usando distancias entre algunas de las ciudades más importantes de este universo, podemos ver cómo estas distancias no solo nos cuentan cuán lejos están entre sí, sino que también nos dan pistas sobre la curvatura del mundo que habitan.
En lugar de limitarnos a imaginar el mapa de Juego de Tronos como algo plano y bidimensional, vamos a dar un paso más y a pensar en términos de geometría esférica. Usando datos de distancias entre ciudades como Volantis, Braavos, y otras, podemos empezar a aplicar algunos principios básicos de la matemática que nos ayudarán a visualizar este mundo de una manera completamente nueva. De esta forma, aunque Juego de Tronos sea una obra de ficción, también podemos apreciarlo desde una perspectiva matemática y científica que lo hace aún más fascinante.
Durante mis años de maestría, uno de los libros técnicos que más me impresionó fue Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity de Steven Weinberg. En la introducción de este libro, Weinberg aborda la fascinante historia de las geometrías no euclidianas, un concepto que cambió profundamente nuestra comprensión del espacio y la distancia. Me quedó grabado su análisis sobre cómo las distancias entre cuatro puntos en una superficie plana siguen una relación específica. Es impresionante cómo estas distancias no son simples, sino que obedecen a una ecuación compleja que refleja la naturaleza intrínseca de las superficies planas.
Lo que me llamó particularmente la atención fue cuando Weinberg presentaba ejemplos de esta teoría aplicados a un mapa muy conocido: el de la Tierra Media de J.R.R. Tolkien. En su libro, Weinberg muestra las distancias entre varias ciudades clave en la Tierra Media, como Hobbiton, Erebor, Dagorlad, y la Ciudad de los Corsarios. Las distancias entre estas ciudades, que varían entre 735 y 1498 millas, se relacionan de forma similar a la ecuación que describen las distancias en una superficie plana.
Las distancias eran como:
- $d$(Hobbiton, Erebor) = 813 mi
- $d$(Erebor, Dagorlad) = 735 mi
- $d$(Dagorlad, City of Corsairs) = 780 mi
- $d$(City of Corsairs, Hobbiton) = 1112 mi
- $d$(Hobbiton, Dagorlad) = 960 mi
- $d$(Erebor, City of Corsairs) = 1498 mi
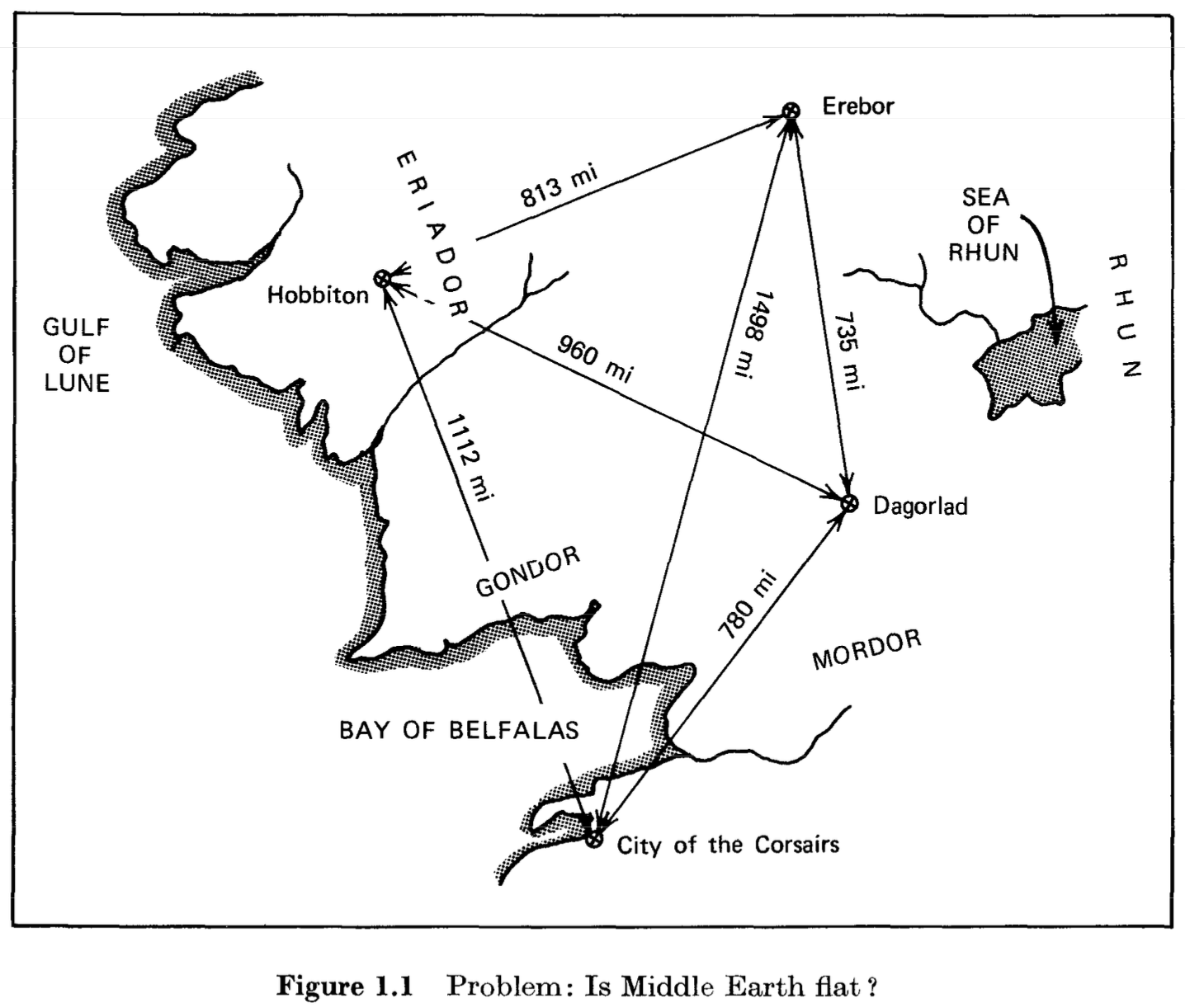
Lo curioso es que esta misma relación de distancias, aplicada a un mundo ficticio como la Tierra Media, nos brinda una excelente oportunidad para explorar conceptos más profundos de geometría no euclidiana. Así como Weinberg utilizó las distancias de la Tierra Media para ilustrar un concepto matemático, nosotros podemos aplicar este mismo enfoque al mundo de Game of Thrones, para demostrar que no es plano, sino que tiene una curvatura esférica. Al comparar estas distancias en un mundo ficticio con principios matemáticos reales, podemos hacer un puente entre la ciencia y la fantasía, revelando una perspectiva completamente nueva sobre los mundos que amamos.
Cálculo de las Distancias y el Determinante
El determinante de Cayley-Menger es una herramienta fundamental en geometría y física para analizar las distancias entre puntos en un espacio Euclidiano. Este determinante permite determinar si un conjunto de puntos puede colocarse en un plano o si el espacio tiene curvatura, como ocurre en una esfera. El determinante de Cayley-Menger lleva el nombre de dos matemáticos: Arthur Cayley, un geómetra británico especializado en geometría algebraica, y Karl Menger, un joven profesor de geometría en la Universidad de Viena. Menger extendió los resultados algebraicos de Cayley para proponer un nuevo axioma de los espacios métricos utilizando conceptos de geometría de distancias hasta la equivalencia por congruencia. Este axioma dio lugar al determinante de Cayley-Menger, que generaliza una de las primeras fórmulas en geometría de distancias: la fórmula de Herón, que permite calcular el área de un triángulo dado sus longitudes de lados.
El determinante de Cayley-Menger se puede aplicar a un conjunto de puntos en un espacio Euclidiano \(\mathbb{R}^k\) con \(k \geq n\), donde \(n\) es el número de dimensiones del simplex. En un espacio bidimensional o tridimensional, este determinante se utiliza para calcular el volumen de un triángulo o un tetraedro, respectivamente, a partir de las distancias entre los puntos. Para cuatro puntos \(( A_0, A_1, A_2, A_3 )\) en \(\mathbb{R}^k\), el determinante de Cayley-Menger se define como (https://en.wikipedia.org/wiki/Cayley–Menger_determinant):
\[\Delta_{CM}(d_{ij}) = \begin{vmatrix} 0 & d_{01}^2 & d_{02}^2 & d_{03}^2 & 1 \\ d_{01}^2 & 0 & d_{12}^2 & d_{13}^2 & 1 \\ d_{02}^2 & d_{12}^2 & 0 & d_{23}^2 & 1 \\ d_{03}^2 & d_{13}^2 & d_{23}^2 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{vmatrix} = 0\]Donde \(d_{ij}\) son las distancias Euclidianas entre los puntos \(A_i\) y \(A_j\). Si este determinante es igual a cero, las distancias entre los puntos pueden ser consistentes con un plano. Si no es igual a cero, el conjunto de puntos no está en un plano, sugiriendo que el espacio tiene curvatura.
Cálculo del Volumen de un Simplex
El volumen \(V\) de un simplex (como un triángulo en 2D o un tetraedro en 3D) en \(\mathbb{R}^n\) se puede calcular usando el determinante de Cayley-Menger. Para un tetraedro en 3D, el volumen \(V\) está relacionado con el determinante de Cayley-Menger de la siguiente forma:
\[288V^2 = \Delta_{CM}(|\mathbf{x}_i - \mathbf{x}_j|)\]Donde \(\mathbf{x}_i\) y \(\mathbf{x}_j\) son los vectores que representan las posiciones de los puntos. El determinante \(\Delta_{CM}\) nos da una medida del volumen del tetraedro, y si este volumen es cero, entonces los puntos no están en un espacio tridimensional regular (es decir, no están en un plano o una esfera).
Dado cualquier conjunto de 6 números \(\alpha_{ij} \in (0, \pi)\), con \(0 \leq i < j \leq 3\) que satisfacen un conjunto apropiado de desigualdades triangulares. ¿Cuál es la condición adicional que debe cumplirse para tener 4 puntos \(q_0, \dots, q_3\) en la esfera unitaria \(S^2\) tal que la distancia geodésica \(d(q_i, q_j) = \alpha_{ij}\)?
Parametrizamos la esfera unitaria \(S^2\) con coordenadas polares:
\[[0, \pi] \times [-\pi, \pi] \to (\theta, \phi) \mapsto (\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta) \in S^2 \subset \mathbb{R}^3\]Una vez que hemos calculado el volumen del simplex utilizando el determinante de Cayley-Menger, el siguiente paso es calcular los valores de \(e_1\), \(e_2\) y \(e_3\). Esto es similar a parametrizar la esfera. Estos valores son fundamentales porque nos permiten determinar la curvatura del espacio en el que se encuentran los puntos, y en última instancia, calcular el radio de la esfera que podría contener estas distancias.
Para calcular \((e_1, e_2, e_3)\), primero debemos expresar las distancias en términos de los ángulos entre los puntos. Esto se puede hacer usando la fórmula de la ley de los cosenos esféricos para calcular los ángulos \(\phi_i\) entre los puntos en la superficie de la esfera:
\[\cos \phi_i = e_{jk}\]Aquí, ( i, j, k ) son índices que representan las permutaciones de los puntos, y ( e_{jk} ) es la relación de los ángulos calculados entre las distancias entre los puntos en cuestión. Una vez calculados estos ángulos, los valores ( e_1, e_2, e_3 ) se pueden obtener de la siguiente manera:
\[e_1 = \cos(\phi_{12} - \phi_{13})\] \[e_2 = \cos(\phi_{13} - \phi_{23})\] \[e_3 = \cos(\phi_{12} - \phi_{23})\]Estos valores nos proporcionan la relación entre los ángulos y las distancias de los puntos, lo que nos da una representación precisa de la curvatura del espacio.
Finalmente, para determinar el radio de la esfera en la que se encuentran estos puntos, usamos la ecuación siguiente, que involucra las distancias \(d_{ij}\) y los valores de \(( e_1, e_2, e_3 )\):
\[1 - e_1^2 - e_2^2 - e_3^2 + 2 e_1 e_2 e_3 = 0\]Esta ecuación debe cumplirse para que las distancias entre los puntos puedan ser mapeadas sobre la superficie de una esfera.
Aplicación al Mundo de Game of Thrones
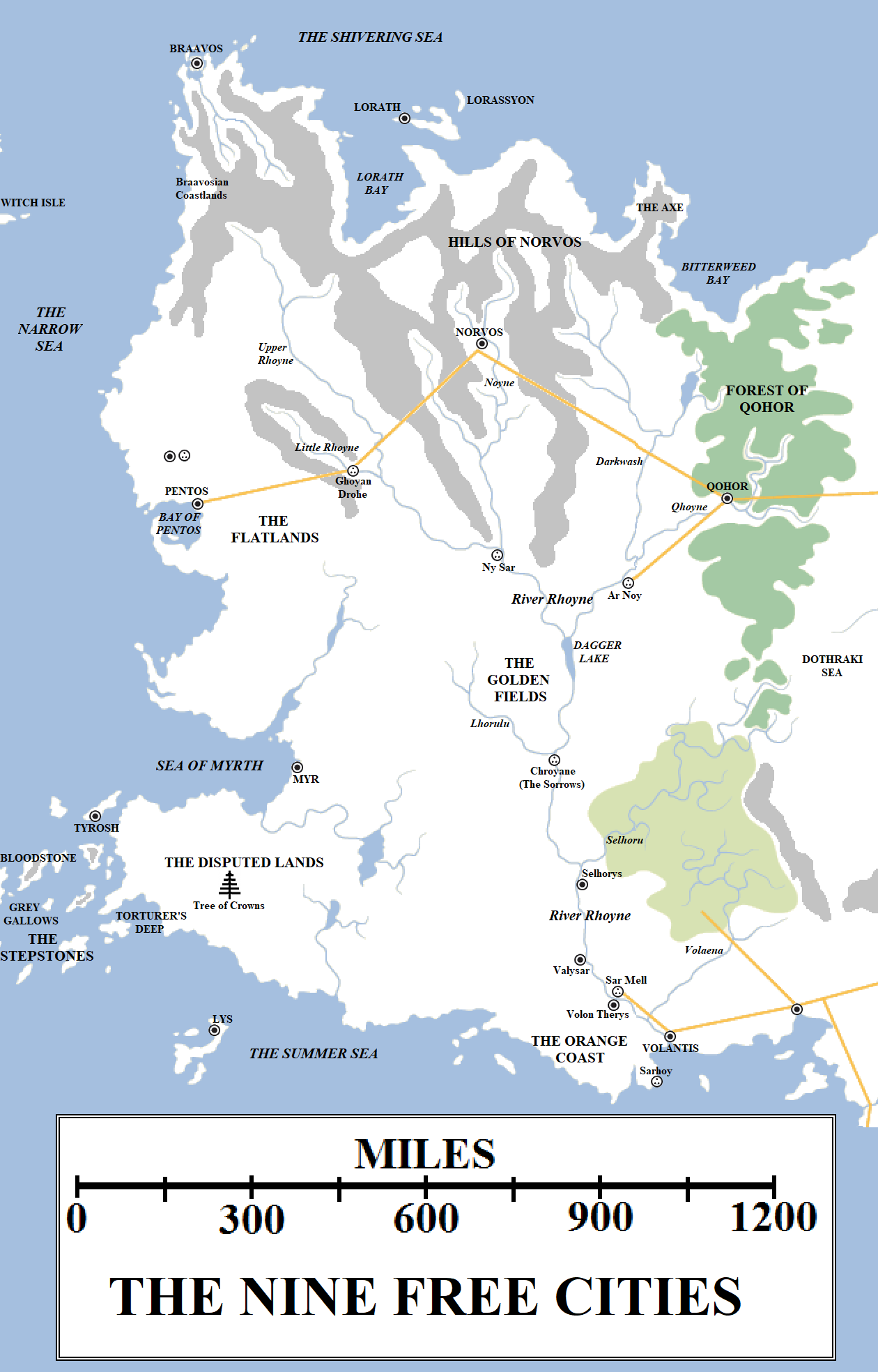
Para aplicar este concepto al mundo de Game of Thrones, primero debemos calcular las distancias entre las ciudades clave del mundo ficticio, como Pentos, Bravvos, Qohor y Volantis. Usando el determinante de Cayley-Menger, podemos verificar si estas ciudades pueden ubicarse en un plano, o si el espacio en el que se encuentran tiene curvatura, lo que sugiere que el mundo de Game of Thrones podría ser esférico. De esta manera, el determinante de Cayley-Menger nos permite hacer una distinción clara entre un espacio plano y uno curvado utilizando solo distancias simples entre puntos. Las distancias son ahora las cuales ha sido obtenidas luego de leer detallada y minuciosamente https://www.worldanvil.com/w/got-rewritten/a/travel y https://atlasoficeandfireblog.wordpress.com/2017/08/20/geographic-map-15-the-free-cities/:
- \(d\)(Pentos, Bravvos) = 720 mi
- \(d\)(Pentos, Qohor) = 900 mi
- \(d\)(Pentos, Volantis) = 1200 mi
- \(d\)(Bravvos, Qohor) = 1200 mi
- \(d\)(Bravvos, Volantis) = 1900 mi
- \(d\)(Qohor, Volantis) = 900 mi
Para hacer esto he preparado un pequeño código para hacer todo. Se ve como sigue.
import numpy as np
from scipy.optimize import fsolve
#dij_values = np.array([1112, 960, 813, 735, 1498, 780]) ## Middle Earth´s world (J. R. R. Tolkien)
dij_values = np.array([720, 900, 1200, 1200, 1900, 900]) ## Game of Thrones´s world (George R. R. Martin)
# Given values of dij (in the problem statement)
d01,d02,d03,d23,d13,d12=dij_values[0],dij_values[1],dij_values[2],dij_values[3],dij_values[4],dij_values[5]
from scipy import linalg
DCM = np.array([[0,1,1,1,1],
[1,0,d01**2,d02**2,d03**2],
[1,d01**2,0,d12**2,d13**2],
[1,d02**2,d12**2,0,d23**2],
[1,d03**2,d13**2,d23**2,0]])
print("El Determinante de la matriz de las distancias es: ",linalg.det(DCM))
if linalg.det(DCM)<0:
print("**El determinante de Cayley-Menger es Negativo**")
print("No es posible colocar los cuatro sitios en un espacio euclideo plano en R2, los puntos están en un esfera")
if linalg.det(DCM)==0:
print("Los cuatro sitios se encuentran en un espacio euclideo plano en R2")
print("El determinante de Cayley-Menger es Nulo")
El resultado de esto es:
"El Determinante de la matriz de las distancias es: -2.4229520927999995e+18"
Luego podemos hacer ahora el cálculo de los radios con el siguiente código:
# Function to calculate e1, e2, e3 based on the formula
def calculate_ei(R):
a01,a02,a03,a23,a13,a12=d01/R,d02/R,d03/R,d23/R,d13/R,d12/R
a31=-a13
e1 = (np.cos(a23) - np.cos(a02) * np.cos(a03)) / (np.sin(a02) * np.sin(a03))
e2 = (np.cos(a31) - np.cos(a03) * np.cos(a01)) / (np.sin(a03) * np.sin(a01))
e3 = (np.cos(a12) - np.cos(a01) * np.cos(a02)) / (np.sin(a01) * np.sin(a02))
e_values = [e1, e2, e3]
return e_values
# Function to solve for R based on the given equation for ei
def equation_to_solve_for_R(R, dij_values):
e_values = calculate_ei(R)
e1, e2, e3 = e_values
# The equation to solve: 1 - e1^2 - e2^2 - e3^2 + 2*e1*e2*e3 = 0
return 1 - e1**2 - e2**2 - e3**2 + 2*e1*e2*e3
# Refining the search to find multiple solutions for R
R_initial_guesses = np.arange(500, 6000, 100) # Different initial guesses to try to find multiple solutions
# Store all the R solutions
R_solutions = []
# Solve for R using different initial guesses
for R_guess in R_initial_guesses:
R_solution = fsolve(equation_to_solve_for_R, R_guess, args=(dij_values))
R_solutions.append(R_solution[0].round(4))
R_solutions=np.array(R_solutions)
print("Las únicas soluciónes son: ",np.unique(R_solutions[R_solutions>0])) # Return all the estimated R values
Lo cual da como resultado:
"Las únicas soluciónes son: [ 172.085, 649.9242, 754.432, 2598.1423]"
Conclusiones
Tras aplicar el método matemático del determinante de Cayley-Menger a las distancias entre las ciudades clave del mundo de Game of Thrones, hemos logrado obtener cuatro posibles soluciones para el radio de las esferas que podrían representar la curvatura del espacio en este mundo ficticio. Las soluciones obtenidas son:
- $R_1 \approx 172.085 \, \text{mi}$
- $R_2 \approx 649.9242 \, \text{mi}$
- $R_3 \approx 754.432 \, \text{mi}$
- $R_4 \approx 2598.1423 \, \text{mi}$
Estas soluciones indican que, en realidad, el mundo de Game of Thrones no es plano, sino que tiene una curvatura esférica. Las distancias entre las ciudades no siguen un patrón lineal que se asociaría con un espacio plano, sino que presentan una estructura que puede ser mejor comprendida mediante la geometría esférica.
El hecho de que existan múltiples soluciones para el radio sugiere que, dependiendo de las distancias consideradas y de cómo interpretamos la geografía del mundo de Game of Thrones, se pueden ajustar diferentes modelos de esferas que representen ese espacio. La diversidad en los radios también puede reflejar variaciones en el modo en que se miden las distancias o en cómo se interpreta la topografía del mundo.
Esta exploración matemática nos permite ver más allá de lo que se muestra en los mapas y nos invita a pensar en la geometría del mundo de Game of Thrones desde una perspectiva científica. Aunque este es un mundo ficticio, aplicar conceptos matemáticos reales como el determinante de Cayley-Menger y la geometría esférica nos da una nueva forma de visualizarlo, convirtiendo lo que parecía ser solo una fantasía literaria en un problema matemático tangible.
En resumen, a través de este análisis, hemos demostrado que el mundo de Game of Thrones es, en efecto, esférico, y que podemos usar herramientas matemáticas para analizar incluso los mundos más fantásticos de manera rigurosa. Esta intersección entre la matemática y la ficción no solo abre nuevas maneras de comprender las historias que amamos, sino que también resalta el poder de la ciencia para desentrañar secretos ocultos en cualquier universo, real o imaginario.